Mühendislik öğrencileri veya direkt olarak mühendisler tarafından iyi anlaşılmadığını düşündüğüm terimlerin başında geliyor rijitlik. Bu yüzden de rijitliğin ne olduğundan ve hangi türleri olduğundan bahsedicem bu yazıda.
Rijitlik
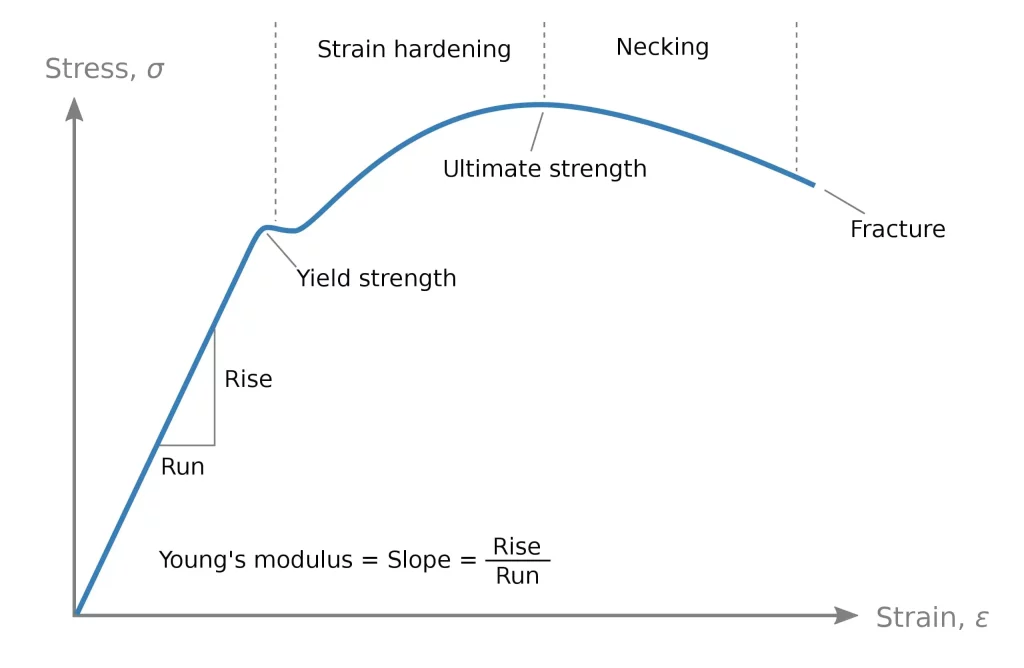
Rijitlik bir malzemenin, cismin, yapı elemanın, yapının, taşıyıcı sistemin vs şekil değiştirme, yer değiştirme, deformasyon gibi eylemlere karşı gösterdiği dirençtir. Yukarıdaki grafikten örnek verecek olursam; yukarıdaki grafik çelik bir çubuğun gerilme – birim şekil değiştirme grafiğini temsil ediyor diyebiliriz. Bu malzeminin rijitliğini ise elastisite modülü ile tanımlayabiliriz. Bu modülün formülü ise:
\begin{equation}
E\text{-}Modul=\frac{Normal~Gerilme} {Birim~Şekil~Değiştirme}
\end{equation}olarak ifade ediliyor.
E-Modul = rijitlik olarak düşünürsek de bir malzemenin rijitliğinin formülü:
\begin{equation}
Rijitlik=\frac{Normal~Gerilme} {Birim~Şekil~Değiştirme}
\end{equation}diyebiliriz.
(2)’deki formülü de:
\begin{equation}
Rijitlik=\frac{Kuvvet} {Şekil~Değiştirme}
\end{equation}olarak genelleştirebiliriz.
Normal Kuvvet Rijitligi
Bulduğumuz bu rijitliği bir malzeme için değil de bir kesit için düşünürsek bu kesitin farklı yükler için farklı rijitlikleri bulunması gerekiyor. (2) formülünü kesitin alanı A ile çarparsak:
\begin{equation}
Kesitin~Normal~Kuvvet~Rijitliği=\frac{Normal~Kuvvet} {Kesit~Alanının~Şekil~Değiştirmesini}
\end{equation}bulmuş oluruz.
Yukarıda da rijitlik = E-Modul demiştik. Bu formülden de bir kesitin normal kuvvet rijitliğinin E-Modul çarpi kesit alanına denk olduğunu bulmuş olduk, yani:
\begin{equation}
Normal~Kuvvet~Rijitliği = E*A
\end{equation}
Eğilme Rijitliği (Bending Stiffness)
Bir kesitin momente karşı rijitliği (Bending Stiffness) için: Bir kesite etkiyen moment sonucu kesitte meydana gelen normal gerilme:
\begin{equation}
Normal~Gerilme = \frac{Moment*x} {Atalet~Momenti}
\end{equation}olarak hesaplanır.
X burada kesitte stresini hesapladığımız noktanın kesitte momentten dolayı stres oluşmayan aksa (Neutral Axis) olan mesafesidir. Biz bu formülü önceden bulduğumuz E-Modul formülü (1) ile birleştirirsek kesitin momente karşı rijitliğinin formülünü de elde etmiş oluruz. İki formülü, (1) ve (6), birleştirince:
\begin{equation}
E\text{-}Modul = \frac{\frac{Moment*x} {Atalet~Momenti}}{Birim~Şekil~Beğiştirme}
\end{equation}buluruz.
Bu formülü biraz düzenleyince de:
\begin{equation}
Moment = \frac{E\text{-}Modul * Atalet~Momenti * Birim~Şekil~Değiştirme} {x}
\end{equation}elde ederiz.
Burada Birim Şekil Değiştirme / X belki size bir anlam ifade etmiyor olabilir ancak bu formül Eğrilik teriminin tanımı aslında. Eğrilik de moment sonucu oluşuyor kesitte. Yani kesite etkiyen moment dolayısı ile kesitte oluşan şekil değişimi. Formülü biraz daha toparlayınca:
\begin{equation}
Moment=E\text{-}Modul * Atalet~Momenti * Eğrilik
\end{equation}ortaya çıkar.
Yukarıda (3) rijitliğin genel tanımını yaparken de:
Kuvvet = Rijitlik * Şekil~Değiştirme
olarak yapmıştık.
Bu formülle karşılaştırma yaparsak da;
Moment = Kuvvet
\\~
\\Eğrilik = Şekil~Değiştirme
\\~
\\Rijitlik = E\text{-}Modul * Atalet~Momentisonucuna ulaşıyoruz.
Yani:
\begin{equation}
Kesitin~Eğilme~Rijitliği=E\text{-}Modul * Atalet~Momenti
\end{equation}sonucuna ulaştık.
Yukarıda gösterdiğim gibi basit mekanik bilgilerini/formüllerini birleştirerek diğer kuvvetlere karşı kesit rijitliklerini de hesaplayabilirsiniz.
Yanal Kuvvet Etkisindeki Kolonun Rijitliği
Malzeme ve kesit rijitliği gibi eleman veya taşıyıcı sistem rijitlikleri de hesaplanabilir. Eleman rijitliği olarak tek başına duran bir kolon düşünün. Bu kolon tek tarafından ankastre olarak mesnetlensin ve diğer ucuna da yanal kuvvet olarak tekil bir kuvvet etki ediyor olsun. Bu kuvvete karşı bu kolonun rijitliği ise:
\begin{equation}
Yanal~Rijitlik = \frac{3*E\text{-}Modul * Atalet~Momenti } {(Kolonun~Yüksekliği)^3}
\end{equation}bulunur.
Sonuçtan da görüleceği üzere eleman rijitliği hesaplarken elemanların boyutları da rijitliğe etki ediyor. Uzun bir kolonun yanal kuvvet rijitliği o kadar da yüksek değilken, aynı kesite sahip kısa bir kolonun rijitliği daha yüksek oluyor.
Rijitlik İle Karıştırılan Terimler veya Konular
Rijitliğin tersi esnekliktir, katiyen süneklik değildir. Süneklik ve rijitlik arasında bir bağ yoktur. Türk mühendisleri bu ikisini zıt terim olarak kullanmayı çok seviyor ancak gerçekte durum böyle değil. Bu konu hakkında daha detayli bir yazı yazıcam yakın gelecekte. Rijitlik ve sünekliğin ne tür bağları olduğunu veya olmadığını o yazıda tartışıcam. Ben o yazıyı yazana kadar net olarak bilebilirsiniz ki rijitliği artırmak için sünekliğin azalması gerekmiyor. Sünekliği sabit tutarak rijitliği artırabilirsiniz. Bir elemanın rijitliğini artırmaya calışırken o elemanın sünekliği azalabilir ama bunun nedenleri farklı. Bu nedenleri bilirseniz ve ona göre dizayn ederseniz, süneklikten ödün vermenize gerek yok. Rijit bir yapı gevrek bir davranış göstermek zorunda değil ve ani göçme yaşamak zorunda da değil. Bir yapı veya eleman aynı anda hem rijit hem de sünek olabilir. Bu konulara değindiğim iki makalemin makale 1, makale 2 linkini bırakıyorum buraya, isterseniz okursunuz onları da.
Sormak istediğiniz sorular varsa bunları yorumlarda sorabilirsiniz.
Hatırlatma: Yazılan makalelerden haberdar olmak istiyorsanız, sosyal medya hesaplarımızı takip edebilirsiniz.