Kelime anlamı olarak mesnet dayanak anlamına gelir. İnşaat mühendisliğinde de yapı elemanlarının başka yapı elemanı veya zemine olan bağlantılarını modellemek için kullanılır. Yani bir yapı elemanı diğer elemanın dayanağı olur ve onu destekler.
Çeşitlerine ve özelliklerine geçmeden önce mesnet reaksiyonları ve serbestlik dereceleri hakkında genel bilgi vermeliyim. İki boyutlu mesnetlerde (yaylar hariç) üç tane serbetlik derecesi ve üç tane de reaksiyon kuvveti bulunur, yani toplamda altı tane bilinmeyen bulunur. Bunlara karşılık da her mesnette sadece üç tane denge denklemi yazılabilir. Altı bilinmeyeni bulmak için ise bu üç denge denklemi yeterli değildir. Mesnetler aslında bize bu altı bilinmeyeni üç bilinmeyene düşürmek için üç tane “ön bilgi” verir. Bu ön bilgiler ve denge denklemleri ile de altı bilinmeyen de bulunmuş olur.
İki boyutlu bir mesnette üç tane reaksiyon bulunur demiştik. Bunlar; yatay ve düşey mesnet reaksiyonu ve moment reaksiyonundan oluşur. Aynı şekilde de üç tane serbestlik derecesi vardı. Bunlar da yine yatay ve düşey yer değiştirme ve moment sonucu dönmedir.
Bu yazıda kullanacağım semboller ise;
\underline{Reaksiyon~Kuvvetleri}
\\~
\\~
A_H = Yatay ~Kuvvet~(H\text{=:}~Horizontal)
\\~
\\~
A_V = Düşey ~Kuvvet~(V\text{=:}~Vertical)
\\~
\\~
M = Moment
\\~
\\~
\\~
\\~
\underline{Yer~Değiştirmeler}
\\~
\\~
u = Yatay ~Yer~Değiştirme
\\~
\\~
w = Düşey ~Yer~Değiştirme
\\~
\\~
φ = DönmeSabit Mesnet
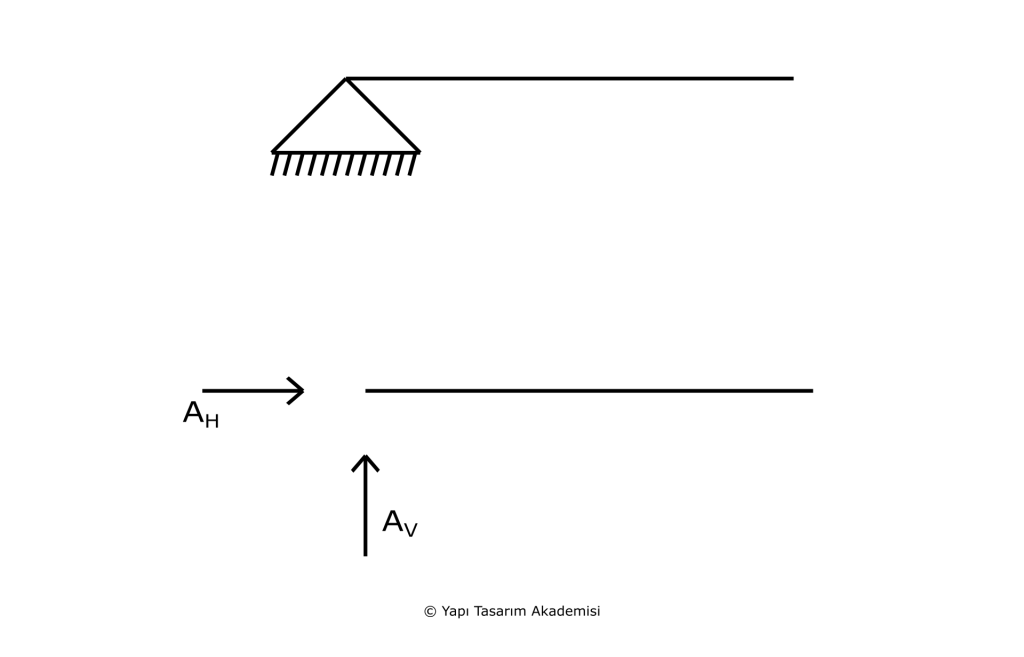
Sabit mesnet, mesnet noktası etrafinda serbest bir şekilde dönebilir. Serbest bir şekilde dönebildiği için de mesnette moment meydana gelmez. Yatayda veya düşeyde ise hareket edemez, yani u ve w sıfıra eşittir. Yatayda ve düşeyde hareket edemediği için de yatay ve düşey reaksiyon kuvvetleri meydana gelir. Özetlemek gerekirse:
\underline{Ön~Bilgiler}
\\~
\\~
M = 0
\\~
\\~
u = 0
\\~
\\~
w = 0
\\~
\\~
\\~
\\~
\underline{Bulunması~Gereken~Bilinmeyenler}
\\~
\\~
A_H \neq 0
\\~
\\~
A_V \neq 0
\\~
\\~
φ \neq 0 Kayar Mesnet
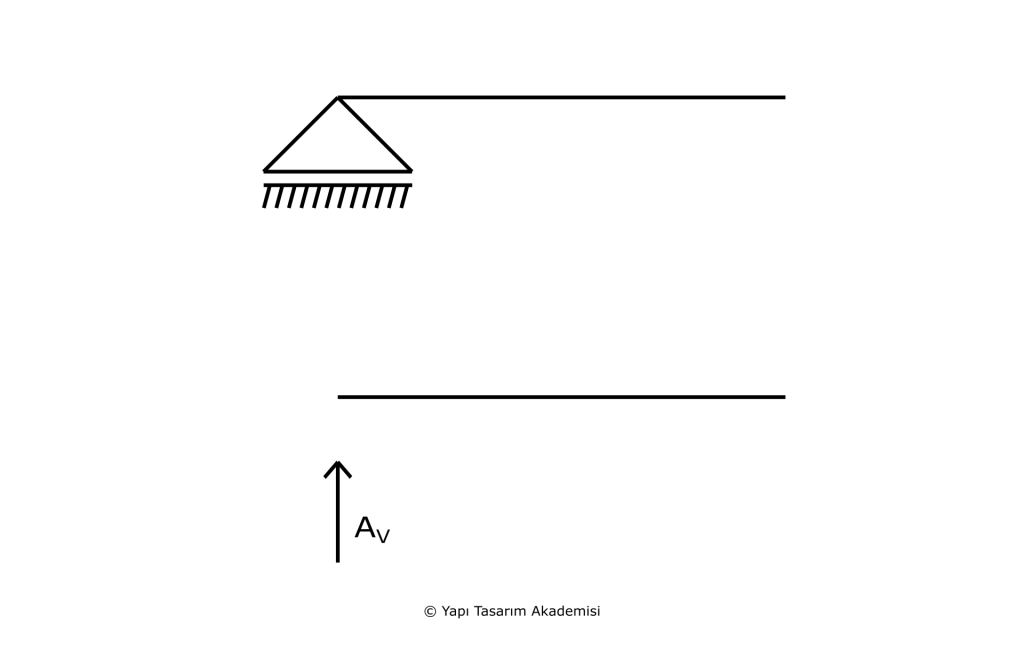
Kayar mesnet, mesnet noktası etrafında serbest bir şekilde dönebilir ve yatayda serbetçe kayabilir. Serbest bir şekilde dönebildiği için de mesnette moment meydana gelmez, serbestçe kayabildiği için de yatay reaksiyon kuvveti meydana gelmez. Düşeyde hareket edemez, yani w sıfıra eşittir. Düşeyde hareket edemediği için de düşey reaksiyon kuvvetleri meydana gelir. Özetlemek gerekirse:
\underline{Ön~Bilgiler}
\\~
\\~
M = 0
\\~
\\~
A_H = 0
\\~
\\~
w = 0
\\~
\\~
\\~
\\~
\underline{Bulunması~Gereken~Bilinmeyenler}
\\~
\\~
A_V \neq 0
\\~
\\~
u \neq 0
\\~
\\~
φ \neq 0 Ankastre Mesnet
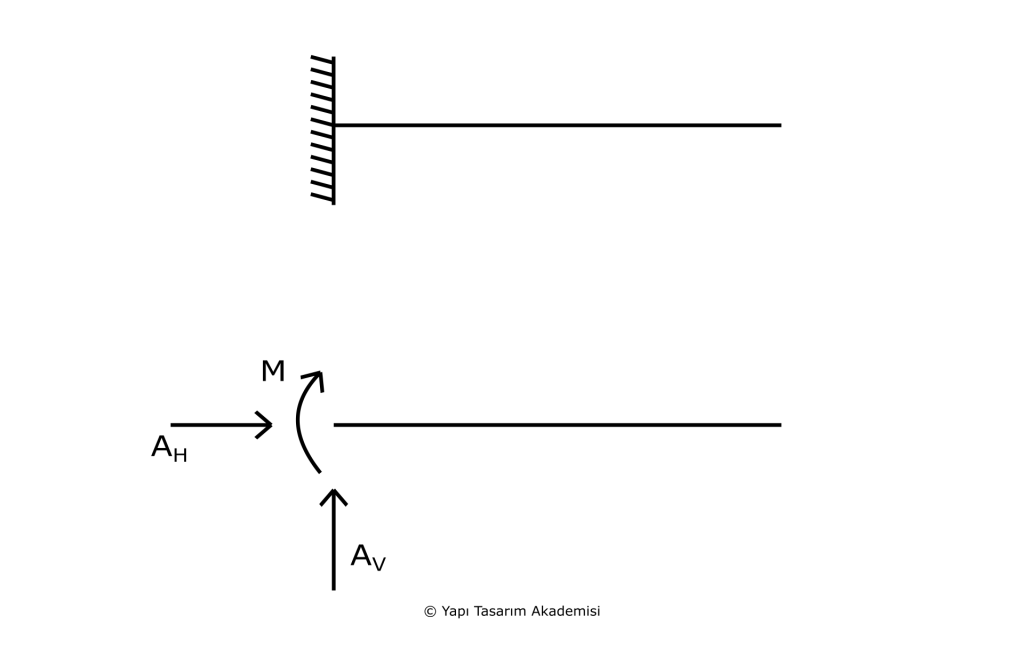
Ankastre mesnette serbest bir şekilde yer değişimi meydana gelmez. Serbest bir şekilde yer değişimi meydana gelemediği için de üç serbestlik derecesinde de reaksiyon kuvvetleri meydana gelir, yani yatay ve düşey kuvvetler ve moment. Serbest bir şekilde yer değiştiremediği için de w, u ve φ sıfıra eşit olur. Özetlemek gerekirse:
\underline{Ön~Bilgiler}
\\~
\\~
u = 0
\\~
\\~
w = 0
\\~
\\~
φ = 0
\\~
\\~
\\~
\\~
\underline{Bulunması~Gereken~Bilinmeyenler}
\\~
\\~
A_H \neq 0
\\~
\\~
A_V \neq 0
\\~
\\~
M \neq 0 Düşeyde Kayar Ankastre Mesnet
Ankastre mesnetten tek farkı düşeyde serbest bir şekilde yer değiştirebilir. Bu nedenle de düşeyde reaksiyon kuvveti meydana gelmez. Diğer yönlerde serbest bir şekilde yer değiştiremediği için de u ve φ sıfıra eşit olur. Özetlemek gerekirse:
\underline{Ön~Bilgiler}
\\~
\\~
A_V = 0
\\~
\\~
u= 0
\\~
\\~
φ = 0
\\~
\\~
\\~
\\~
\underline{Bulunması~Gereken~Bilinmeyenler}
\\~
\\~
A_H \neq 0
\\~
\\~
M \neq 0
\\~
\\~
w \neq 0 Yatayda Kayar Ankastre Mesnet
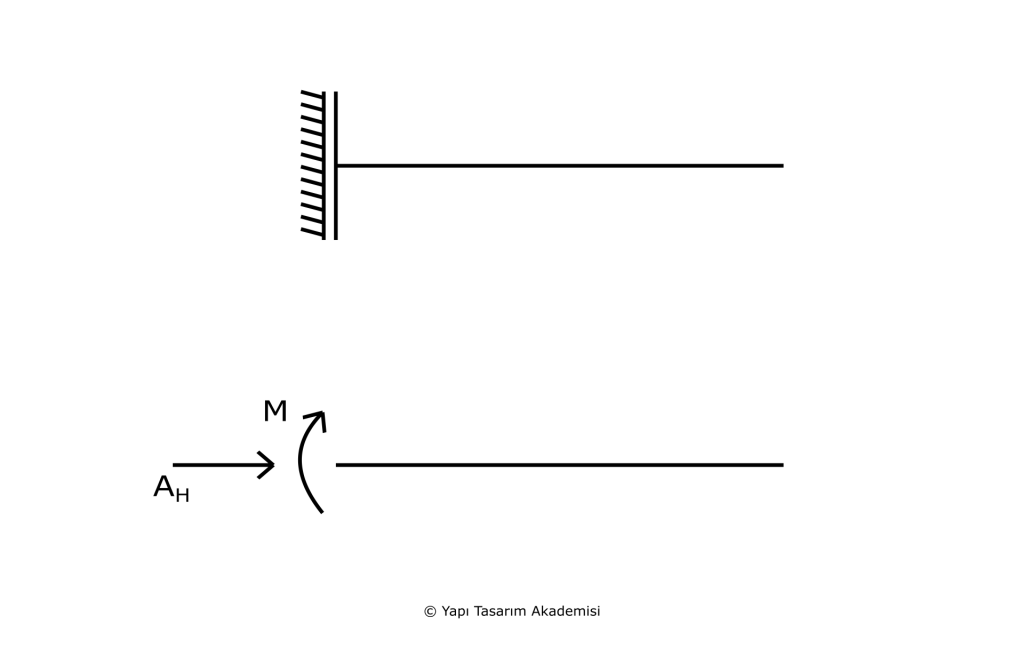
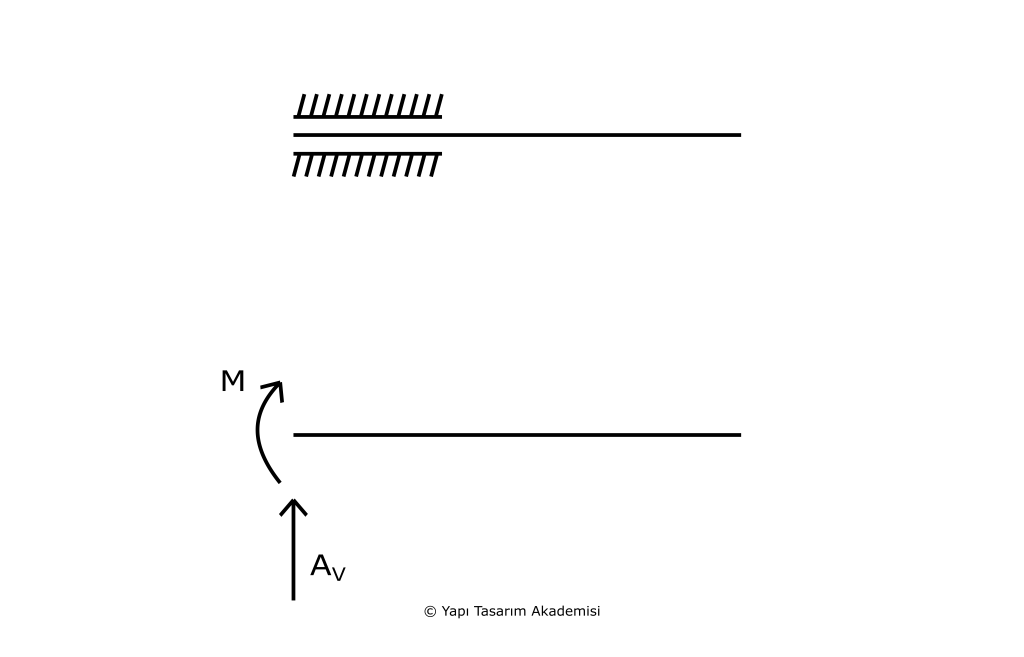
Ankastre mesnetten tek farkı yatayda serbest bir şekilde yer değiştirebilir. Bu nedenle de yatayda reaksiyon kuvveti meydana gelmez. Diğer yönlerde serbest bir şekilde yer değiştiremediği için de w ve φ sıfıra eşit olur. Özetlemek gerekirse:
\underline{Ön~Bilgiler}
\\~
\\~
A_H = 0
\\~
\\~
w= 0
\\~
\\~
φ = 0
\\~
\\~
\\~
\\~
\underline{Bulunması~Gereken~Bilinmeyenler}
\\~
\\~
A_V \neq 0
\\~
\\~
M \neq 0
\\~
\\~
u \neq 0 Elastik Mesnet
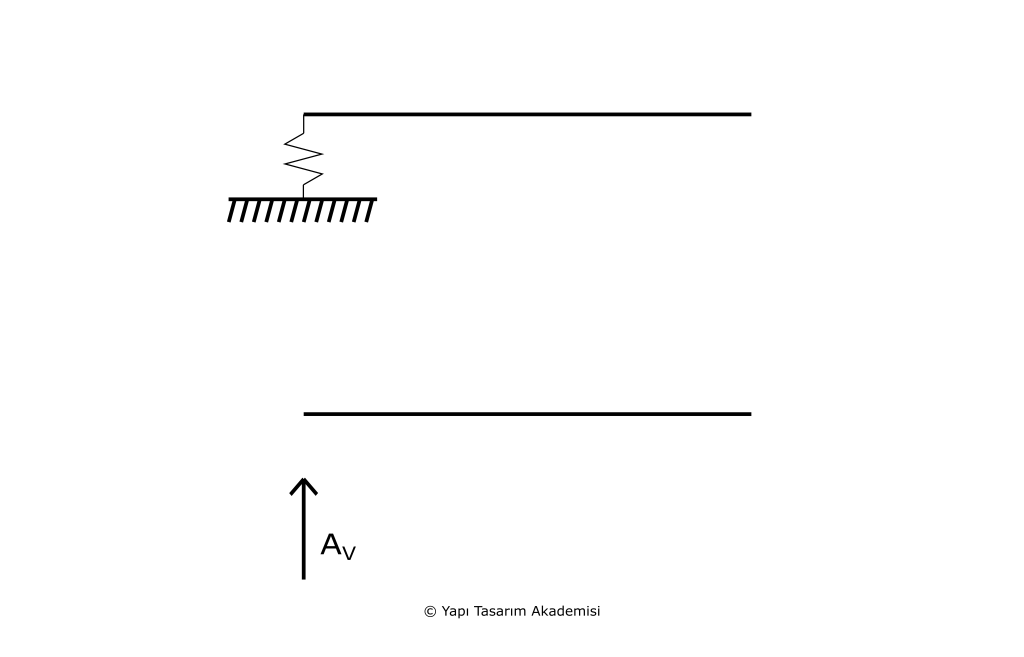
Buraya kadar bahsettiğimiz bütün mesnetler rijit mesnetlerdi. Gerçek hayatta ise sonsuz rijit olan bir malzeme bulunmuyor. Bu nedenle de aslında mesnetleri rijit modellemek “hatalı” bir hareket ama bize oldukça kolaylık sağlıyor. Oldukça rijit olan malzemelerde hata payı çok düşük olacağından rijit mesnet modellemek sorun oluşturmuyor. Ama rijit mesnet ile modellemenin büyük hatalar oluşturduğu durumlarda elastik mesnet kullanabiliriz. Elastik mesnet yay olarak modellenir ve yay katsayısı denen yayın rijitliği cN ile tanımlanır. cN yerine k veya başka bir simge de kullanılabilir. Yaya gelen kuvvet sonucu yayda belli bir yer değişimi meydana gelir. Bu yer değişimi genelde u ile gösterilir ama yukarıdaki u ile karıştırmayın, aynı şeyleri temsil etmiyorlar. U genelde normal kuvvet sonucu meydana gelen şekil veya yer değişimlerini belirtmek için kullanılır. Yaya gelen kuvvetin formülü de:
A_V=F=c_N*u
ile ifade edilir. Yani bu mesnet tipinde yer değişimi ne sıfıra eşittir ne de serbest bir şekilde meydana gelir. Hesap yaparken öncelikle bu mesnet de sanki rijitmiş gibi düşünülür ve bu mesnete gelecek kuvvet hesaplanır. Bulunan kuvvet ile de yayda meydana gelecek yer değişimi hesaplanır:
u=\frac{A_V}{c_N}\underline{Ön~Bilgiler}
\\~
\\~
c_N \neq 0
\\~
\\~
\\~
\\~
\underline{Bulunması~Gereken~Bilinmeyenler}
\\~
\\~
A_V \neq 0
\\~
\\~
u \neq 0 Bu yayı düşeyde değil de yatayda da modelleyebiliriz. Meydana gelecek reaksiyon kuvveti ve yer değişimi de o yönde oluşur.
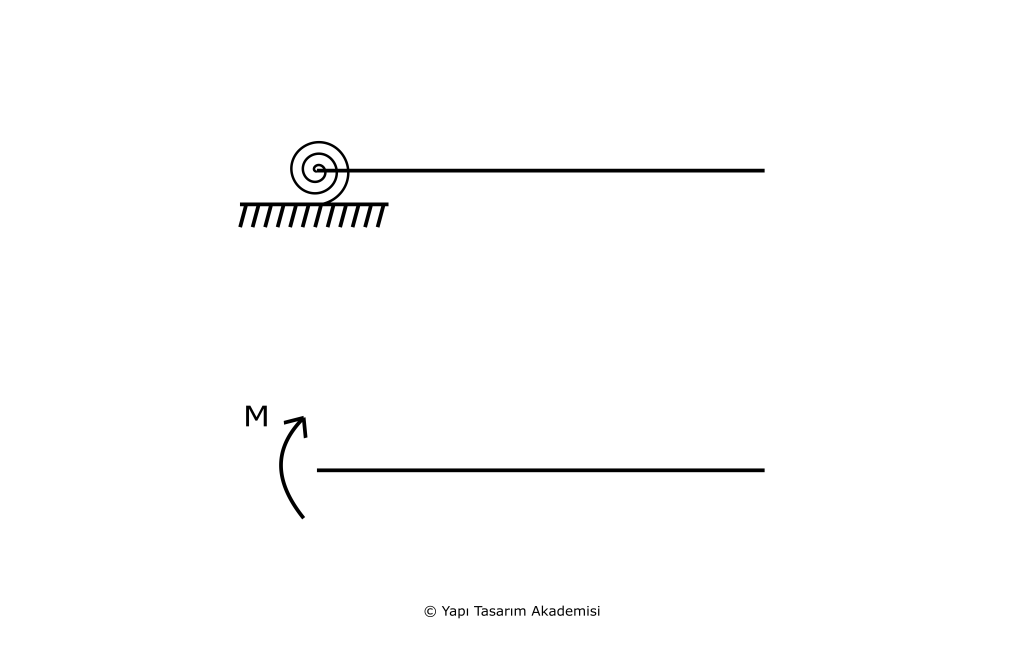
Elastik Moment Mesneti
Elastik mesnet ile aynı mantıkta çalışır, tek farkı sadece momente karşı direnç gösterir. Yay katsayısı cM ile gösterilir. Yayda meydana gelen moment:
M=c_M*φ
formülünden bulunur. Bulunan moment ile de yayda meydana gelecek dönme hesaplanır:
φ=\frac{M}{c_M}Özetlemek gerekirse:
\underline{Ön~Bilgiler}
\\~
\\~
c_M \neq 0
\\~
\\~
\\~
\\~
\underline{Bulunması~Gereken~Bilinmeyenler}
\\~
\\~
M \neq 0
\\~
\\~
φ \neq 0 Sormak istediğiniz sorular varsa bunları yorumlarda sorabilirsiniz.
Hatırlatma: Yazılan makalelerden haberdar olmak istiyorsanız, sosyal medya hesaplarımızı takip edebilirsiniz.
