Bu yazımda sonlu elemanlar metodunun ne olduğunu ve bu metodu baz alarak çalışan programların nasıl çalıştığını anlatıcam kabaca. Bu tarz bir program kullanan her mühendisin detaylı bir şekilde sonlu elemanlar metodunda kullanılan yöntemleri ve elemanları bilmesi gerekiyor ancak bunu bir yazıda yapmak mümkün değil. Üniversitelerde koskoca iki dönem boyunca bunun için ders veriliyor. Ben bu yazıda oldukça temel noktalara değinicem.
Direct Stiffness Method
Her sonlu eleman metodunu kullanan programın temelini oluşturan yöntem olabilir bu yöntem. Bu yöntemde sistem idealize edilmiş parçalara bölünerek ve bu parçaların rijitlik matrizleri tanımlanarak sistem oluşturulur. Yük matrizi ile de yapıya etkiyecek yükler tanımlandıktan sonra elemanların yer değişimleri F = u*k formülünden elde edilir. Normalde bu formüle ekstra bir dış kuvvet için daha terim ekleniyor ama o istisna durumlarda kullanıldığı için göz ardı ettim onu. Bu yöntemde değerler sadece belirlenen noktalarda (node = düğüm noktası) hesaplanır. Bu noktalar dışında bir değeri bilmiyoruz veya hesaplamıyoruz.
Lokal Rijitlik Matrizleri
Yapımızı oluşturacak elemanları rijitlik matrizleri ile tanımlarız. Örnek olarak çubuk elemanları beam (kiriş) veya truss (çubuk) eleman olarak tanımlayabiliriz. Bunların farkları sahip oldukları serbestlik dereceleri ile belirleniyor. Bir kiriş elemanının bükme rijitlikleri bulunurken, truss elemanın bulunmaz. Üç boyutlu bir kiriş elemanının lokal rijitlik matrizinde on iki tane serbestlik derecesi bulunabilir. Bunları x, y ve z yönündeki ötelemeler ve x, y ve z etrafındaki dönmeler olarak tanımlayabiliriz. Bu dediğim altı değeri sahip olduğu her düğüm noktası için lokal rijitlik matrizine yazmamız gerekiyor. Sonuç olarak da on ikiye on iki bir lokal rijitlik matrizi karşımıza çıkıyor.
Sistem Rijitlik Matrizi
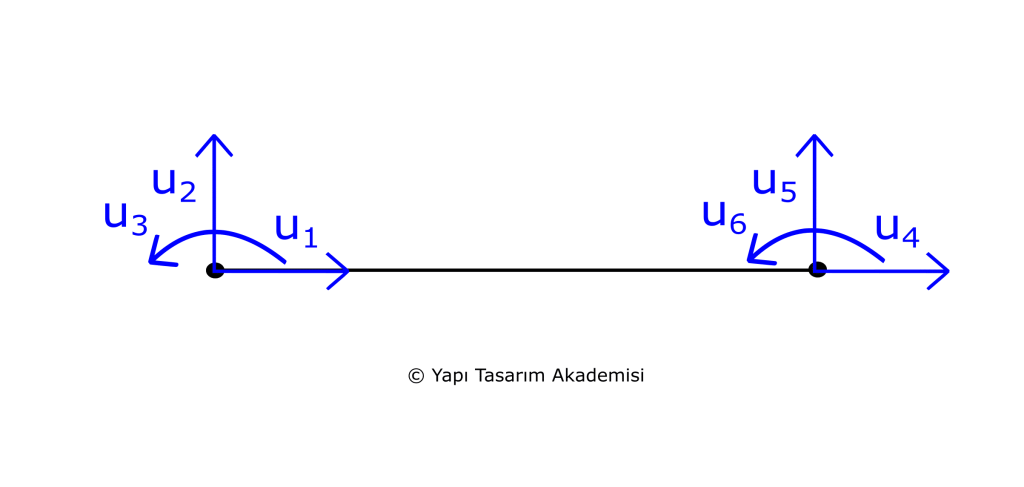
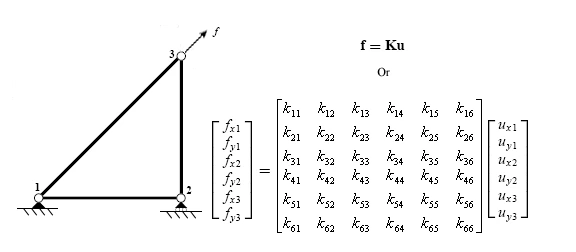
Sonlu elemanlar yönteminde hesaplar global yani sistem matrizi ile yapılır. Her elemanın oluşturulan lokal rijitlik matrizleri rotasyon matrizi ile çarpılarak birleştirilir. Bu birleştirme sonucunda da sistemin sahip olduğu düğüm noktası ve bu noktaların serbestlik derecesi çarpımı büyüklüğünde bir sistem rijitlik matrizi ortaya çıkar. Yukarıdaki resime bakarsanız sistemin üc tane düğüm noktası bulunuyor ve her düğüm noktası sadece iki (x ve y ötelemesi) serbestlik derecesine sahip. Sonuç olarak da sistem rijitlik matrizi altıya altı oluyor. Her türlü hesap da bu sistem rijitlik matrizi ile yapılıyor. Sisteme etkiyecek yük matrizini ve sistem rijitlik matrizini oluşturduktan sonra F = u*k formülünden her bir düğüm noktası için yer değişimleri bulunur.
Sonlu Elemanlar Metodu
Buraya kadar yazdıklarım sadece Direct Stiffness Method’unu anlatıyor Sonlu Elemanlar Metodunun temeli diyebiliriz. Yukarıda hesaplanan değerleri sadece düğüm noktaları için bildiğimizi yazmıştım. Basit problemler için biz differansiyel denklemler kullanarak elemanların sadece başında ve sonunda düğüm noktası oluşturarak eleman boyunca hesapladığımız değerin değişimini bulabiliriz. Ancak karışık sistemlerde bu her zaman mümkün olmuyor, mümkün olsa dahi büyük projelerde oldukça hız kaybına yol açıyor. Bunun yerine sonlu elemanlar metodunda yaklaşık sonuçlar verecek yöntemler kullanılıyor. Bunlardan bir tanesi Galerkin Metodu.
Galerkin Metodu
Çözmemiz gereken problem 3. dereceden bir polinom olsun. Biz bu metodu kullanarak ve çözüm sanki 1. dereceden bir polinommus gibi yaklaşık hesap yapabiliriz. Yaptığımız bu hesabın düğüm noktalarında tam olarak doğru olması gerekiyor çünkü bu hesap sınır şartlarını tam olarak yerine getirmeli. Ancak iki düğüm noktası arasinda hesaplanan değerler gerçek sonuçlardan farklı değerlerde oluyor.
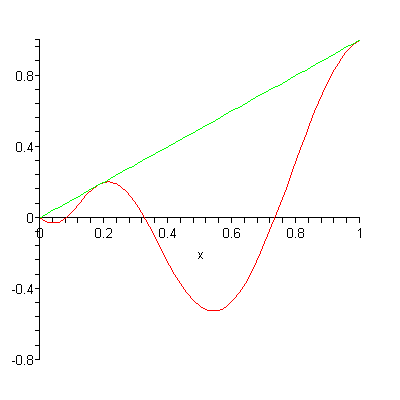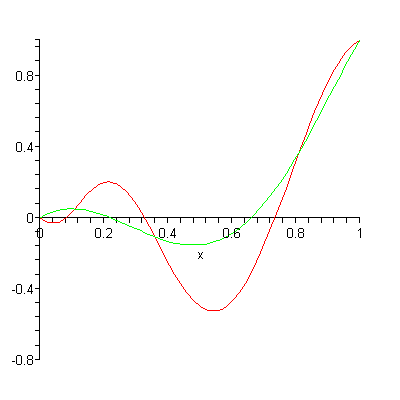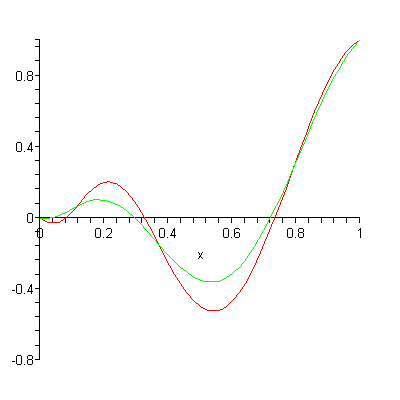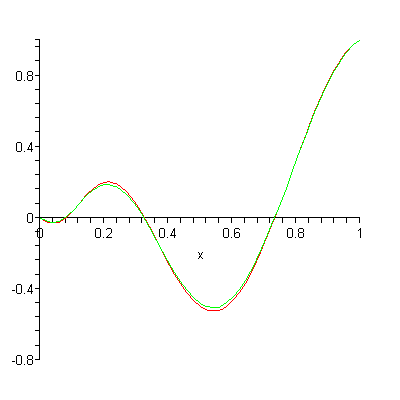
Yukarıdaki gif’e bakarsanız yaklaşık hesap için kullanılan polinomun derecesi artırılınca gerçek sonuç ile daha iyi örtüşüyor. Yaklaşık hesap için kullandığımız polinomun derecesi ve gercek sonucun derecesi aynı ise sonuçlar birebir örtüşür, aksi durumda ise belli bir oranda hata ile yaklaşık hesap yaparız. Ama her durumda sınır şartlarındaki değerleri (örnek için konuşursak başlangıç ve bitiş noktaları) doğru hesaplıyor.
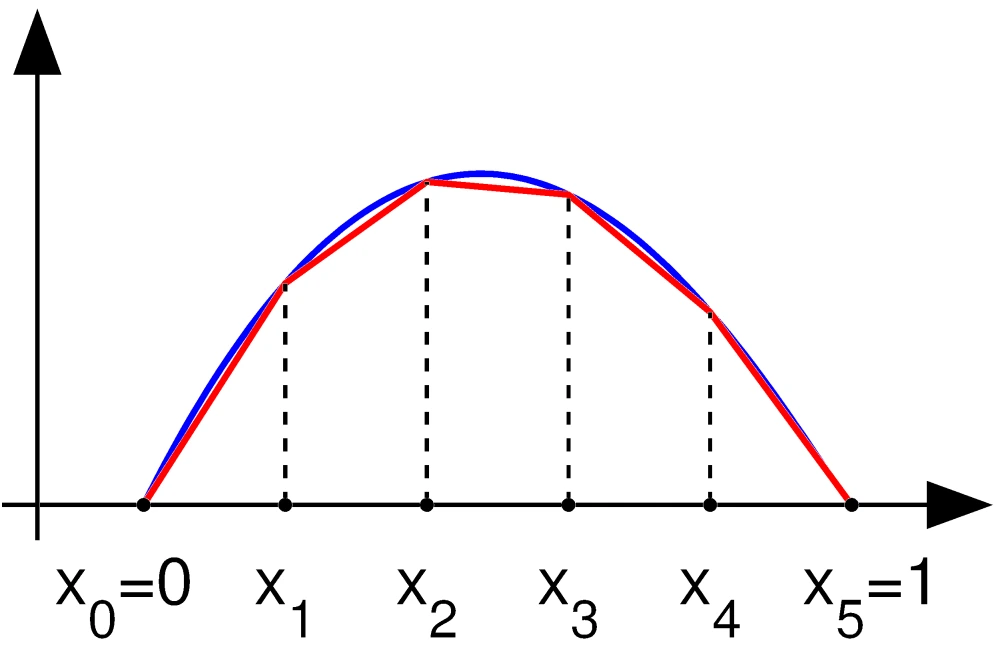
Biz de sadece 1. dereceden bir polinom kullanarak dahi sadece düğüm noktası sayısını artırarak oldukça gerçeğe yakın sonuçlar elde edebiliriz. Yukarıdaki resime bakarsanız ne demek istediğimi çok daha iyi anlarsınız.
Sonlu elemanlar metodunun ana mantığı da budur. Çözümü mümkün olmayan veya oldukça işlem gücü gerektiren bir problemi ufak parçalara bölerek ve yaklaşık olarak hesaplar. Programı kullanan kişi ne yaptığını biliyorsa oldukça doğru sonuçlar alabilir, aksi takdirde ciddi hatalara sonuç açabilir.
Sonlu elemanlar metodunda kullanılan eleman çeşitleri:
Kafes Eleman
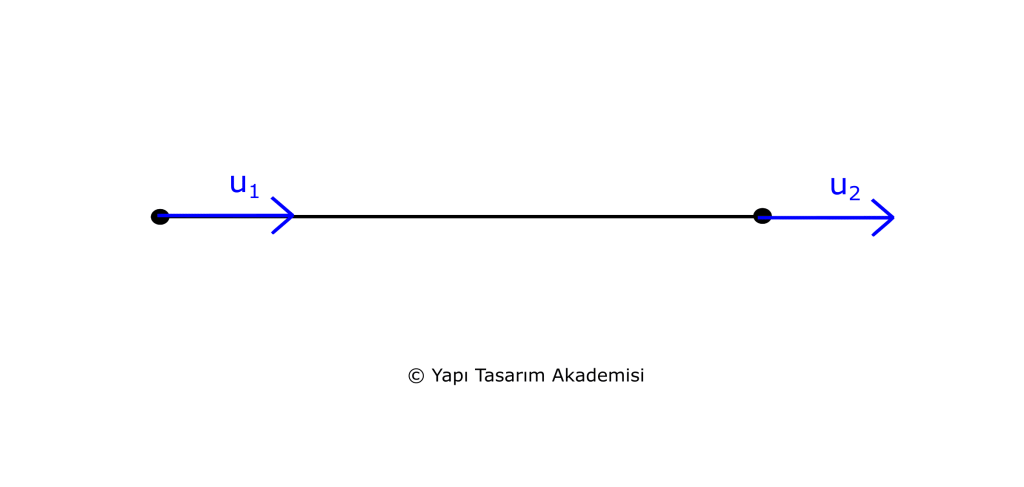
Bu elemanın sadece normal kuvvet etkilerine karşı rijitliği bulunur. Düğüm başına da sadece bir tane serbestlik derecesi olur. Kafes (truss) sistemlerindeki çubukları modellemek için bu eleman kullanılır.
Çerçeve Elemanı
Çerçeve sistemlerin kolon ve kirişlerini modellemek için kullanılır. Düğüm noktası başına üç tane serbestlik derecesi bulunur. Normal kuvvet, kesme kuvveti ve momente karşı rijitliği bulunur.
Levha Eleman
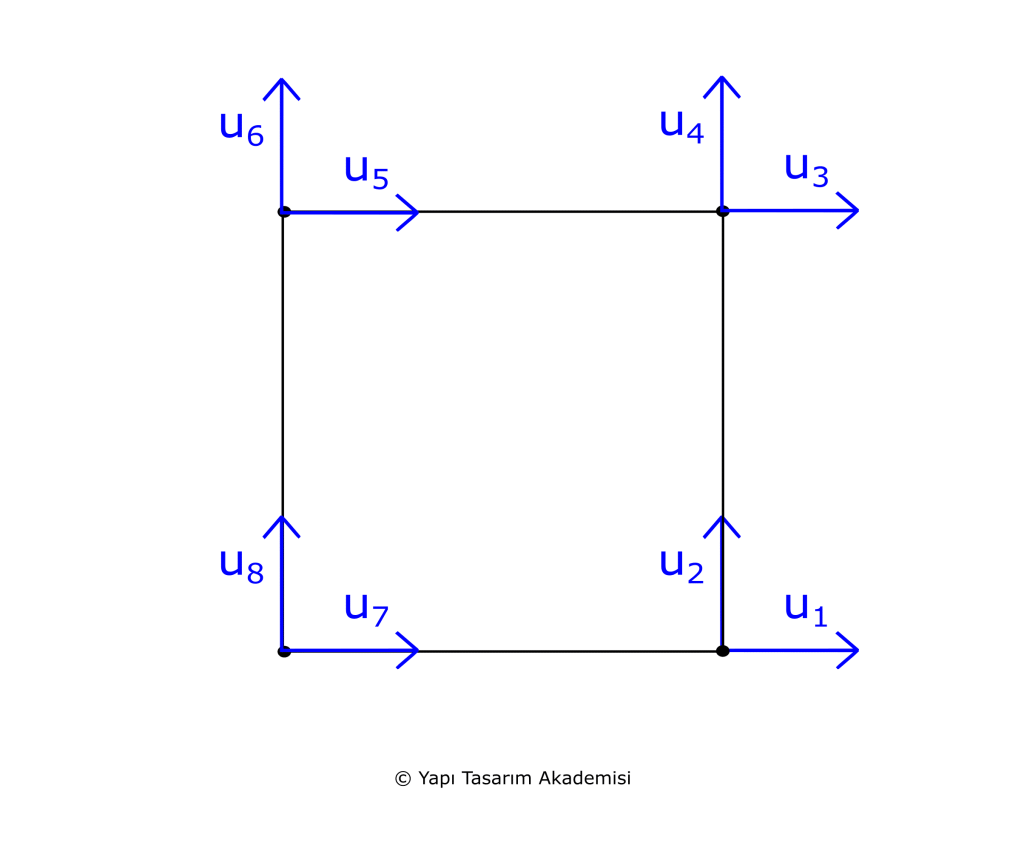
Levha eleman perde duvar gibi elemanları modellemek için kullanılır. Bu elemanın sadece düzlem içi rijitlikleri bulunur. Düzlem dışı rijitlikleri sıfırdır, yani gözardı edilmiştir. Perde duvarların da uzunluğuna göre kalınlıkları oldukça düşük olduğundan düzlem dışı rijitlikleri gözardı edilebilir. Bu elemanı kullanabileceğiniz yapı elemanlarının düzlem içi rijitliğinin düzlem dışı rijitliğine göre çok daha yüksek olması gerekir ve genelde düzlem dışı kuvvet gelmeyecek veya gelen kuvvet gözardı edilebilecek elemanlarda kullanılır. Düzlem içi kuvvetlere membran kuvvetleri de denir.
Plak Eleman
Plak eleman ise levhanın tam tersine sadece düzlem dışı rijitliklerine sahiptir. Döşeme gibi düzlem içi gelen kuvvetlerin gözardı edilebileceği yapı elemanlarının modellemesinde kullanılır. Düzlem dışı kuvvetler ise momentler ve kesme kuvvetleridir.
Kabuk Eleman
Kabuk eleman ise levha ve plak elemanın birleşmesi sonucu oluşan bir elemandır. Yani kabuk elemanın hem düzlem içi hem de düzlem dışı rijitlikleri bulunur. Hem düzlem içi hem de düzlem dışı yük etkiyen elemanlar modellenir kabuk eleman ile. Kabuk eleman ile bütün döşeme ve perde duvar gibi yapı elemanlarını da modelleyebilirsiniz. Bunun size tek dezavantajı işlem yükünün artması olacaktır.
Hatırlatma: Yazılan makalelerden haberdar olmak istiyorsanız, sosyal medya hesaplarımızı takip edebilirsiniz. Sormak istediğiniz bir şey varsa yorumlar kısmında bunu sorabilirsiniz.